Frame Interpolation is great. Don't use it to "improve" animation!

---

Ach ja, you probably all know that one annoying friend complaining about your TV settings, right?. You don’t? Well, allow me to introduce myself. My name is HansiMcKlaus and if I see another one of those 60FPS interpolated anime fights, I will fucking snap. But more importantly, I want to shed some light on the nature and technical aspects of frame interpolation, instead of just complaining about it. I may not be whatever the video equivalent of an audiophile is, but I do care about certain aspects of the video process and how adjustments change the way we literally view things.

If you are a fan of interpolated video, good for you. I may spit on your grave, but I will not blame anyone for liking it. At the end of the day, it is a preference like any other. However, there is an underlying science to it and I want to explain the causes and effects interpolation has. So, let’s talk some math!

Signal processing

Okay, let’s start with the basics. Most things can be viewed as some kind of a signal, the most obvious ones being light and sound, but it also includes less “natural” phenomena like, as a matter of fact, most if not all kinds of information imaginable over time. A clock makes a signal beyond the indication of time by the ticking of the second hand and so does a body by simply existing. What the signal entails depends on the use case, but the main take-away is that “framerate” is not quite a signal, though I will explain in what way exactly later.

There are two kinds of signals, analog and digital ones. Analog signals are continuous in time, while digital signals are quantized to discrete values. Most “natural” signals are analog, while most recordings and readings of a signal are digital. Digital doesn’t mean that it is made on a computer, by the way.

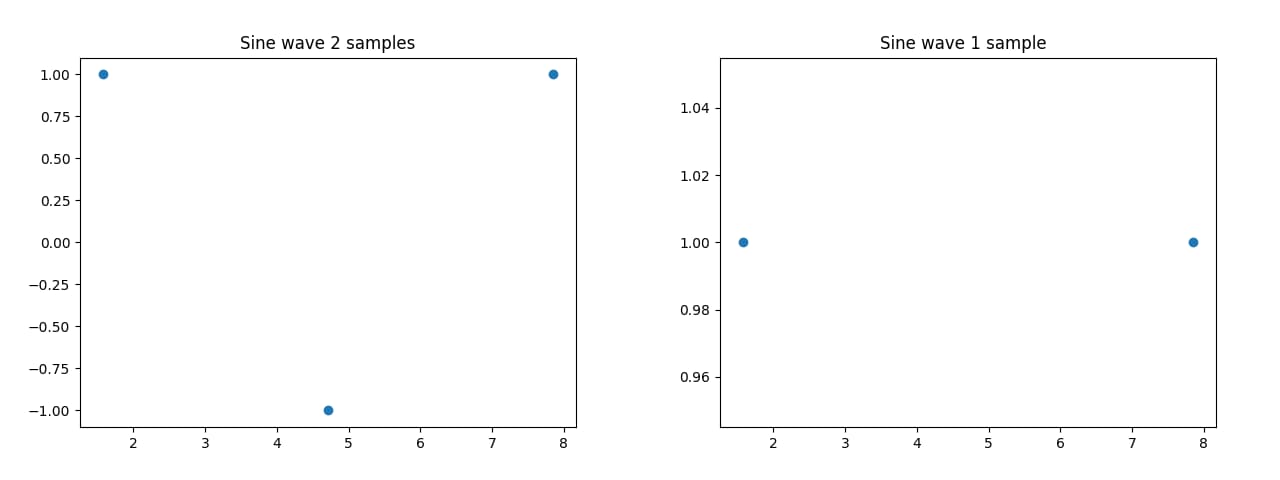
Imagine a sine wave. A sine wave continuously changes its value between 1 and -1 over time. We can convert this analog signal into a digital one via approximation. For that, we simply record the value of the sine wave at certain points in time. In this example, the samples at time 0 and 2π are technically the same and the latter one is only there for illustrative purposes, if you are wondering why there is always one more sample than stated.

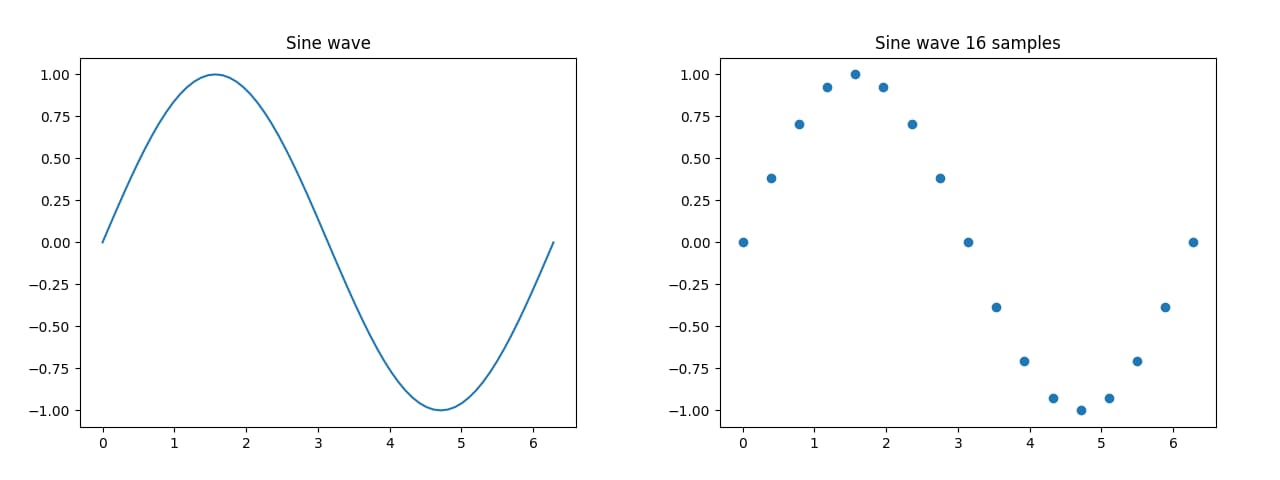
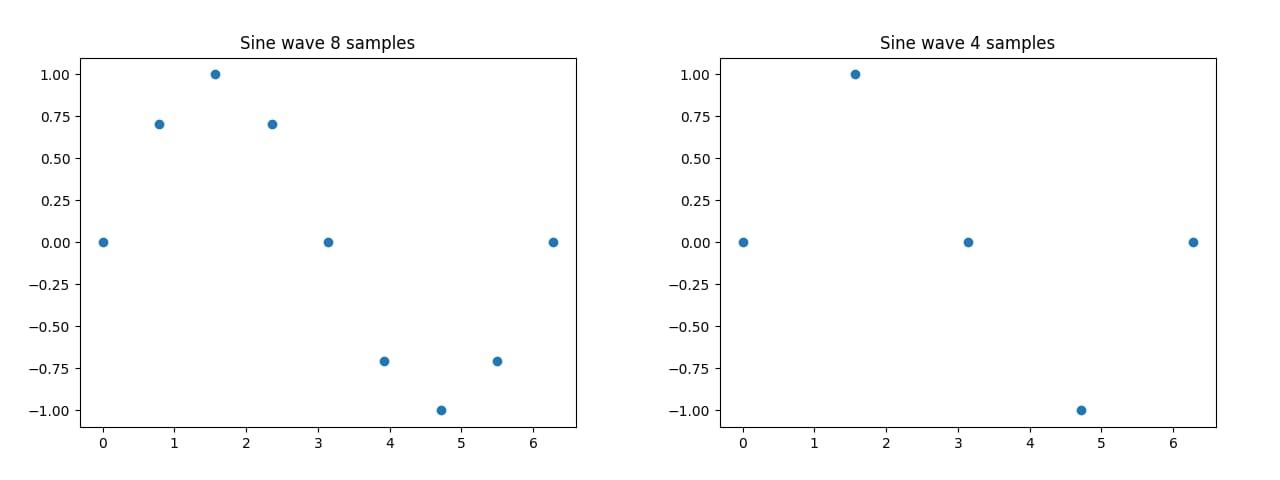
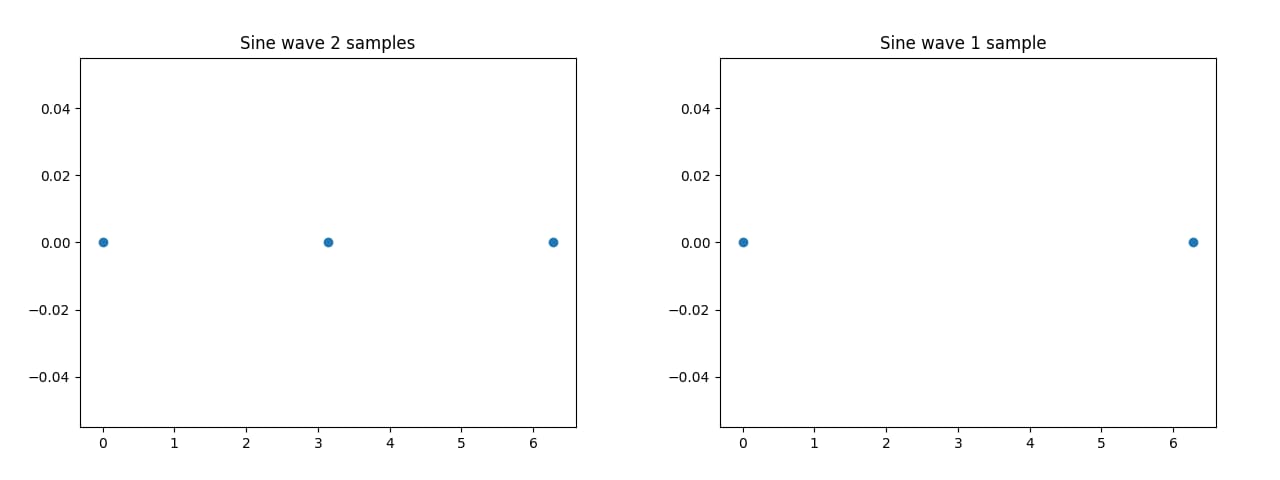
The number of samples we take for each time period is the samplerate. As we can see, the lower the samplerate, the less accurate the digital signal is to the analog one, until it is no longer recognizable at all in the last graph. Introducing the “Nyquist–Shannon sampling theorem”. In short, it describes a condition for when a digital signal is able to contain all the information of its analog signal counterpart. It basically comes down to the fact, that the samplerate has to be at least twice the highest frequency in the signal.

So, for our sine wave example with the frequency of 1/2π (A full circle of a sine wave is defined over 2π), our samplerate has to be at least twice of that, resulting in a samplerate of 2/2π or simply π, meaning that if we take the value of the sine wave at every π, it results into an accurate approximation of said curve. On first inspection, this doesn’t seem to be quite correct, as both the last two graphs (Samplerate of π and 1/2π) seem to only contain a constant value. This, however, is simply a result of the starting point of the sinus function. If one were to shift the curve, you can see how the left graph with the samplerate of π (2 samples) does in fact resemble a (crude) sine wave plus the correct frequency, while the right graph with one sample doesn’t.

If the samplerate is not high enough, you may get these weird artefacts like when recordings a propeller and the blades seem to spin backwards or very slowly. The Nyquist–Shannon sampling theorem also explains, for example, why digital audio tends to have a samplerate of 44.1K or 48K, since the human ear can hear frequencies up to 20KHz, meaning that at least a samplerate of 40KHz is required with slightly more added due to other technical aspects of audio.

Upscaling and Interpolation

Ok, since we are mostly working with digital signals, we also know that our signals are approximations at a specific resolution called a samplerate (or any other term). We have also seen that a higher samplerate tends to result in a more accurate representation of the analog source. Unfortunately, recording a signal at a “high” samplerate is not always possible, either due to simple availability of the signal, technical constraints in the recording itself, or a lack of space to record the signal onto – Ever seen how large FLAC files or uncompressed video can get? – so it is possible that our digital signal is too low resolution/has a too small a samplerate and needs to be up-scaled or, in the case of audio, up-sampled.

Interpolation works by filling “gaps” between a pair of discrete values with another artificially created values not originally found in the recorded signal. There are many sophisticated types of algorithms for interpolation, depending on the type of signal and in recent years, trained networks also made a big leap in providing good up-scaling capabilities. Personally, I use waifu2x for upscaling anime-style images and am pretty happy with it. However for this post, let’s look at arguably the simplest type of interpolation: Linear interpolation.

Linear interpolation works by simply taking a value between the two values adjacent to its position, in the easiest case the average, but also “weighted”, depending in its relative position between the next adjacent values. For example, you have two values, 1 and 5 and want to interpolate this sequence to contain five values. Depending on your implementation, this interpolated sequence could be 1,3,3,3,5 or 1,2,3,4,5… it’s very simple.

Going back to our sinus curve example, here are the up-sampled (by a factor of 4) waves of samplerates 16/2π and 4/2π with the red dots being the new samples introduced by the interpolation, now containing 64 and 16 samples respectively.

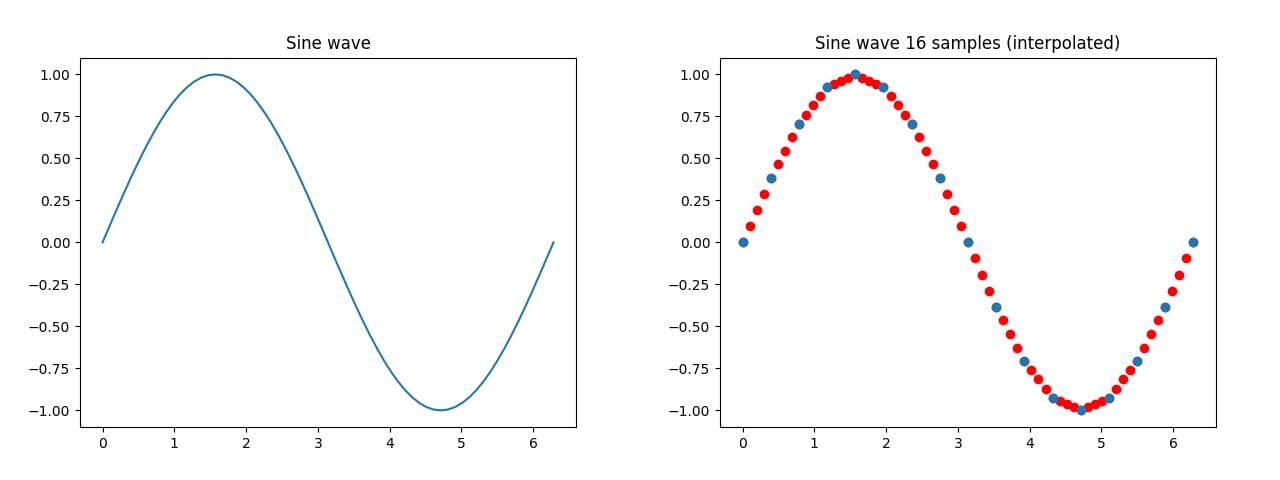
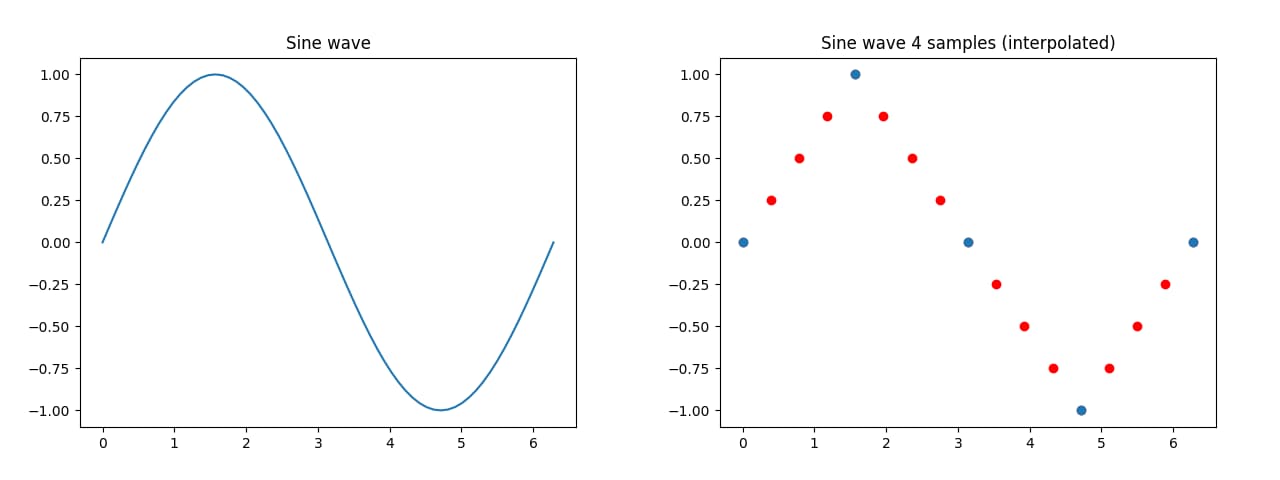
In both cases, we could have simply connected the dots via a straight line… well, it is called linear interpolation for a reason. However, while not perfect, every red dot is closer to the actual value of the sine wave at each time, compared to as if you were to take one of the blue values, making it more accurate by reducing the average error.

Arguably, this graph of a sine wave may not be the best example to show the results of up-scaling in a real-life context. Unfortunately, I wasn’t able to program my own up-sampler for audio (that actually worked well), so I kindly refer to a demo by Volodymyr Kuleshov. As we can see hear, the interpolated audio, while not great, is definitely better than the one with the low samplerate.

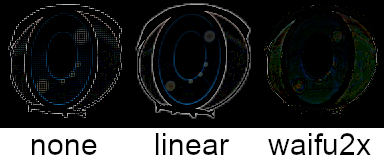
I never acknowledged it until now, but images are also signals and can be up-scaled, here by nearest neighbor interpolation (also known as none), linear interpolation and waifu2x:

Note how the first two interpolation techniques lose a bit of “sharpness”. The first one displays the exact same information on a larger area, making it appear “pixelated”. The second one loses its contours by averaging the edges with the areas around them. These effects become more obvious the higher the uscaling factor (here 2) is. Waifu2x, being based on a trained network, is able to counter these artefacts and creates an image that is pretty close as to how the original image would look like at the same resolution. Here is a difference map with the new images subtracted from the “original”

Working with limited samples

Ok, why don’t we just interpolate everything if the results become better (given an adequate interpolation)? Well, similar as to why we don’t record every signal in the highest samplerate possible: We can’t always do that. This is also especially true when creating signals under severe technical limitations, like creating a video game in the 80s. You don’t create playable character and simply downscale them to fit the small boundary of only a couple of pixels. Instead, you created Pixelart.

Pixelart is a weird beast, going against the very nature of analog signals. Until now, we have only discussed signals, that try to approximate an analog signal into a digital one. This is not the case with pixelart, as pixelart has no analog counterpart to itself. The discrete values are the fully realized representation of the signal with no loss in accuracy whatsoever. You can still up-scale pixelart, but you will not gain any useful new information from doing so and, depending on the type of interpolation, may even worsen the result. Pixelart and everything else created on the basis on limiting the samples is already in its best form available.

The reason I took pixelart as an example is because I think it is a rather easy example to grasp. The point isn’t always to maximize the numbers of samples available, but work within a certain range to create a specific effect. While pixelart is a result of the inherent limitations of old hardware, it still survived the shift into modern times on the basis of it looking awesome. Pixelart has a certain appeal to it that HD images and highly detailed 3D models simply can’t replicate and it found its way into a specific kind of aesthetic. (Hopefully) no one will go around and claim that pre generation 6 Pokémon would look better, if all the sprites were large anti-aliased drawings. While pixelart wasn’t always an artistic choice, the result still stands as its own with absolutely no need for up-scaling.

If one wants to get real technical about things, you could argue that every rasterized image is technically pixelart, but the point is to differentiate images that are limited in samples by design and those that are simply low on samples. You can see that in different techniques of creating pixelart, like intentionally down-sampling real-life recordings or 3D renders to create a pixelart effect. Also, while the concept of time is continuous, there is a smallest interval of time in a physical sense (247 zeptoseconds is the lowest ever recorded). However, considering such a short time span is basically not perceivable by any human, it doesn’t change the fact that there is a difference in analog and digital signals. You could still say something happens every zeptosecond. Real life has no framerate!

Frame Interpolation

Any type of video is simply a sequence of individual frames played back fast enough to create the illusion of motion. This is true for real life recordings, as well as artificially created videos like animation. Frame interpolation creates new frames between already existing ones, essentially increasing the framerate of the video. Framerate is our samplerate when talking about video, mostly measured in frames per second (FPS).

There are several reasons why one might want to create a higher framerate video. In its easiest form, more frames correspond to a smoother playback, as the “distance” between two frames decreases the more frames are created inbetween. This can also create the effect of movement with higher/slower framerate appearing faster, due to smaller noticeable changes, despite taking the same amount of time.

This smoothness isn’t even specific to just interpolated video, but all video with a “high” framerate. One time, I have seen a commercial in what I guess were 60FPS, as opposed to the standard 24/30FPS I am used to and was like “damn, these motion graphic are smooth”. However, I don’t want to talk about the benefits of high framerates or the soap opera effect (Which probably has a good amount of impact on how one perceives interpolated video), as maybe this is a topic for another time and I want to keep the focus on interpolation.

Now, here is the kicker: I absolutely adore the technical aspects of frame interpolation and what stunning effects one can achieve with them, with slow-motion being the most obvious one. It works surprisingly well on sport clips and anything where the camera might not “catch up” to the human eye.

This video shows off some clips using Google’s Large Motion Frame Interpolation and in my humble opinion, ignoring some artefacts, this looks great and I am all for it. However, my problems with frame interpolation start when applied to animation.

You remember my short tangent on pixelart? Let’s talk about how framerate itself is not a signal and why animation works. This may be more of a simple technical detail, but framerate is simply the samplerate of the signal (video), with the signal being the information inside the frames. However, despite working in the time domain, I think, concerning interpolation, it is important to acknowledge how the signals changes when altering the framerate, as opposed to simply adding more samples in the sine wave example, as it visibly changes the signal, or at least how it is perceived.

The second aspect of this is the idea of frames and framerate in the realm of animation. Similar to pixelart, animation has no “real” analog signal to compare or approximate down to. A frame of animation is not a snapshot of how the animation would look at this point in time, but the frame simply is how the frame looks. Obviously, the idea of a frame is still to portray the idea of motion in time, but it doesn’t have to follow any real-life logic, even when animating realistic movement. The artist has full control over the frame.

This brings up the question: To what do you even interpolate animation? Well, one basically does it under an assumption, similar to how you would interpolate real life footage. Since animation still portrays motion, it is possible to generate a frame that would gap its two adjacent frames, hopefully resulting in a smoother playback and as long as the original animation isn’t completely wild in its movement, this is indeed the case… at the cost of breaking the animation most of the time.

Here is the thing. Animation doesn’t (have to) follow movement that would make sense physically from a timing perspective. Since animation is not based on an analog signal, you can simply create two frames with a character snapping from one pose to another and while you could interpolate those frames to follow what should have been the logical movement, this is not what the animation portrayed.

Animation is created in a limited space, seldom exceeding a framerate of 24FPS with no obligation to use every single frame on a new unique frame. There is animating on 2’s, 3’s, 4’s and so on, meaning that only every n-th frame is unique, resulting in a perceived framerate even lower than the initial 24FPS. While the reason for the relatively “low” amount of frames is the insane amount of labour involved in creating animation, this is not an inherent flaw, as artists came up with techniques to give their animation a sense of movement and appeal, despite it.

I often don’t like it when one simply refers to the “12 principles of animation” as the end all for animation, but they do show most important aspects of animation and we can see how most of these principles are affected by interpolation. Interpolating frames will mess with anticipation and follow-through, ruin slow ins and outs and throw the complete timing of key poses out the window. Animation is made while accommodating the framerate and also able to change it on the spot. Just blindly interpolating animation will alter the source in a way, that no longer supports the techniques that made it work in the first place. This is not even mentioning stuff like smears whose purpose is to help simulating clear fast movement under frame constraints (beyond looking great… I love smear frames), that loose its effect, when interpolated. every animation is supposed to be smooth with realistic movement. Sometimes, the appeal is in snappy motion, fast poses and impact. A lot of animators have their own style, that utilize a lower amount of frames to their fullest potential and not in spite of the few frames. And don’t get me started on camera pans, etc, that are added separate from the animation and completely clash when interpolated.

I once came upon this video about a stop-motion animator interpolating their Lego animaton to 60FPS and while I am happy that they are happy about the results, I can not, for the life of it, understand why they, an animator, and a lot of the comments think that this looks better than the original. At the end of the day, it comes down to a matter of personal preference, but I can’t wrap my head around why so many people are fine with these seemingly uncanny interpolated clips.

Something to make clear is that my problem is with the concept of interpolation itself and not the newly generated frames introduced by the interpolation. For now, they look rather bad, being less sharp, worse to read and contain those weird artefacts. It also feels like, especially with anime, frame interpolation tends to rather morph between frames, instead of generating completely new ones. While there is still a lot of work to be done, I have little to no doubts that there will come a time, where those generated frames will look passable, even by my standards. Combine it with programs like TVP Anime Interpolation by Tsubajashi, which is specifically trained on anime footage and the interpolation might at least look decent, even if the timing problem still persists.

Frame interpolation as part of the production

So, what happens when the frame interpolation is not done on the already composited animation, but rather in the corresponding step in the animation process? Introducing programs like Cacani, animation tools for creating inbetween frames and giving the artists the ability to oversee the interpolation process themselves and to correct it. Studios like David Production and Ufotable have used interpolation software to aid in animating difficult scenes and it enables them to try out more complex shots.

All new David Production titles use Cacani for computer-generated inbetweens and it seems like it's affecting how they conceptualize anime - expect more slowmo, rotations, tricky sequences exploiting that. The result isn't always natural (especially on the 1s) but it's intriguing pic.twitter.com/oRqRgbKxG3

— kViN 🌈🕒 (@Yuyucow) October 12, 2018

While I don’t think this clip from JoJo’s Part 5 is a showcase of perfect interpolation, it at least displays the capabilities in adapting interpolation for certain effects. Meanwhile, the following clip of Demon Slayer uses its interpolation to create this very consistent subtle movement that would be almost impossible to draw by hand. Notice how it is animated on 2’s, meaning only every second frame is unique, yet it still feels rather smooth. Turns out smoothness is not only factored by framerate alone. It is not used here, but motion blur can also go a long way.

Those two clips are great examples where frame interpolation has its legitimate use-cases and I am interested in seeing similar approaches used in other series. I genuinely think it is worth looking into stuff like effect animation can gain something from interpolation. Frame interpolation can both reduce the workload of animators, as well as enable more complicated and tricky shots, so we will have to see where it leads us in the future.

Conclusion

I am genuinely impressed by the technical aspects of frame interpolation. I didn’t go quite into the actual technicalities of frame interpolation, as my knowledge and understanding of its inner workings are just to limited. I am, however, able to evaluate the results. At the end of the day, frame interpolation is a tool like any other and should not be confused with a magical “create animation” button. I am simply sick and tired of some dudebros abusing their GTX 1080 Ti to “improve” animation and point at it like “Look! 60FPS! So smooth!” and don’t think about whether it is actually effective in enhancing the experience, or simply a monster brought to live by carelessness and oversight.

And again, there are people that genuinely enjoy interpolated animation, but in my eye, I have yet to see a single clip that looked actively better by interpolating it. I am happy to be convinced otherwise, but until then, I will criticize frame interpolation everywhere I see fit, as if I were on some weird animation-purist crusade.